Roulettes, Part 3

Roulettes

Part 3: Deriving Formulas

We represent our procedure for drawing roulettes in the following diagram.

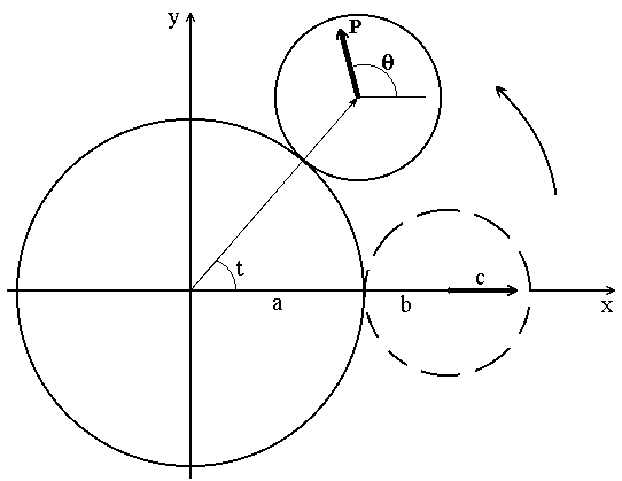
We have a wheel of radius b rolling on the outside of a circle of radius a. The tracing point is at distance c from the center of the rolling wheel. We choose our coordinate system so that the origin coincides with the center of the fixed circle and the center of the wheel is on the positive x-axis. We assume the wheel moves in a counterclockwise direction around the circle. Let t be the angle swept out on the fixed circle.

Find a vector description for the center of the rolling wheel as a function of t.

Now find a description of the vector from the center of the rolling wheel to the position of the point (again, as a function of t). [Hint: How far has the wheel rolled along the circle? What distance on the circumference of the wheel corresponds to that distance? How is theta related to t? Make sure your answer is consistent with the two-coins test in Part 1.]

Finally, find a description for the vector from the origin to the point P as a function of t. From this vector description write parametric formulas x(t) and y(t) for the curve traced out.

Use the plotting commands in your computer algebra worksheet and the parametric description obtained in step 3 to draw the parametric curves for your recorded choices of a, b, and c. Do the plotted curves match the curves you drew with the SpiroGraph applet? If not, revise your parametric descriptions until they model the curves you drew. (You will need to keep the graphs in your report to make a convincing case.)

Experiment with different values of a, b, and c to develop conjectures about the following questions.
- How does the number of loops around the circle before closing depend on the constants a, b, and c?
- How is the number of inner turning points on the curve related to the constants a, b, and c?

Once you are confident of your conjectures, use the parametric descriptions of the curves to show why your conjectures are correct.