Roulettes
Part 4: Hypocycloids and Related Curves (Optional)
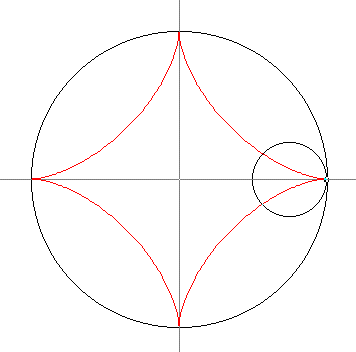
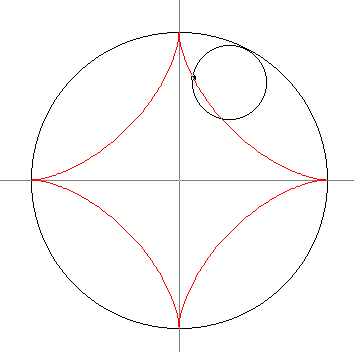
The figure above shows
two views of the construction of a hypocycloid, a curve traced out by
a point on an inner circle as that circle rolls around an outer circle. The
picture on the left shows the starting and ending position, and the one on the
right shows an intermediate position. You can draw such curves with the SpiroGraph
applet by making the second radius (b) negative. If the applet is not
already running, click here. Then
return to this page for further instructions.
- Our four-cusp hypocycloid was
constructed by taking the smaller radius to be exactly one-fourth of the larger
radius. Confirm this by using the applet to reconstruct the figure above.
(You may want to start by enlarging the left-hand circle.) How do you have
to set c to keep the drawing point on the inner circle?
- Experiment by changing the value
of b, both larger and smaller, while keeping the drawing point on the
inner circle. What do you think determines the number of cusps of the hypocycloid?
What about the number of times the inner circle goes around the outer one
until the curve returns to it starting point?
- Experiment by changing the value
of c, both larger and smaller. (These roulettes are no longer hypocycloids.)
Describe what you see, and state any conclusions you draw.
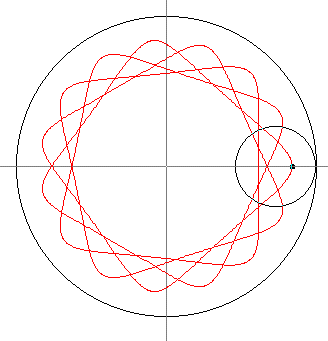
- The following figure shows a curve
that might have turned up in step 3, depending on your choices. Count the
number of "outer turning points," that is, points where the curve
is closest to the fixed circle. What does this count tell you about a,
b, and/or c? You should be thinking about relations between
two or more of the constants, not actual numbers.
- The procedure for finding formulas
for these curves should be very similar to the one you followed in Part 3.
Have you already derived the formulas? Try the values of a, b,
and c you used in steps 2 and 3 -- enter them in the formulas in you
worksheet, and see if the same curves are drawn. If not, how do you need to
modify the formulas to accommodate the rolling circle being on the inside?
- When you're sure you have correct
formulas, revisit your answers to steps 2, 3, and 4. Have you correctly identified
how the relative sizes of a, b, and c determine the different
types of curves?
|
CCP Home | Materials | Multivariable
Calculus | Module Contents | Back
| Forward |