Go to CCP Homepage Go to Materials Page Go to Linear Algebra Materials Go to Table of Contents
Go Back One Page Go Forward One Page

Least Squares

Part 3: The normal equations

If p = b1 + mx is the projection of y onto W = Span(1, x), then we can write

p = Xv,

where X is the matrix with columns 1 and x, and v is the solution vector (b, m)T. Also, the vector y - p is orthogonal to the entire subspace W, in particular, to both 1 and x. This orthogonality can be expressed as

XT(y - p) = 0,

or

XTy = XTp = XTXv.

The system of equations

XTXv = XTy,

in which everything is known except v, constitutes the normal equations. Thus, the coefficients for the best fitting line are the solutions of the normal equations.

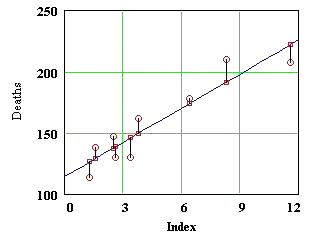
Hanford data with least squares line

  1. Construct the matrix X for the cancer death data, and solve the normal equations. Make sure your numbers m and b agree with what you see in the figure showing the least squares line.

  2. Confirm that your coefficients m and b give the same projection p as the one you computed in Part 2.

  3. If there were a location in the Columbia River area with exposure index 5.5, what would you predict about its cancer death rate? What portion of this death rate would you attribute to radioactive wastes from the Hanford plant?
Go to CCP Homepage Go to Materials Page Go to Linear Algebra Materials Go to Table of Contents
Go Back One Page Go Forward One Page

modules at math.duke.edu