Go to CCP Homepage Go to Materials Page Go to Linear Algebra Materials Go to Table of Contents
Go Back One Page

Least Squares

Part 4: Summary

  1. Suppose you have n pairs of data points,

    (X1,Y1), (X2,Y2), ..., (Xn,Yn).

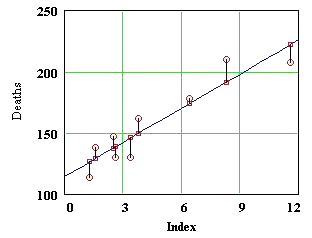
    Describe in your own words the problem of finding the best fitting line for this data. In what vector space can this be formulated as a linear algebra problem? What linear algebra problem is equivalent to finding the coefficients of the least squares line?

    2. Hanford data with least squares line

  2. How are the normal equations constructed from the data? For fitting a line to data, how many normal equations are there, and how many variables do they have?

  3. Suppose X1 = X2 = ... = Xn. What will the matrix X look like? What will the data plot look like? Explain why you would expect the normal equations to be inconsistent in this situation.

  4. What geometric relationship is expressed by the normal equations? Why do the normal equations almost always have a unique solution?
Go to CCP Homepage Go to Materials Page Go to Linear Algebra Materials Go to Table of Contents
Go Back One Page

modules at math.duke.edu