|
|
|
|
f(t) = c1 g1(t) + c2 g2(t) + ... + ck gk(t),
that is, if the model function is linear in the parameters c1, c2, ... , ck of the model. In our quadratic model of Part 1, the component functions used in defining f(t) were g1(t) = 1, g2(t) = t, and g3(t) = t2.
Let's see why the method of Part I works for the more general linear model. Suppose the data points are (Ti, Yi), i = 1, ... , n. Define the following vectors in Rn:
y = (Y1,
Y2, ..., Yn)T
g1 =
(g1(T1), g1(T2), ..., g1(Tn)
)T
,
g2 =
(g2(T1), g2(T2), ..., g2(Tn)
)T
,
...
gk =
(gk(T1), gk(T2), ..., gk(Tn)
)T
.
Then W = Span(g1, g2, ... , gk) is the k-dimensional subspace of Rn of vectors of the form
c1 g1 + c2 g2 + ... + ck gk
The least squares problem is to find values of the parameters c1, c2, ... , ck that produce the vector in W closest to y. This vector is the projection p of y onto the subspace W.
As we saw in Part 1, the
values of the parameters that minimize the distance from y to W
are the components of the vector
v = (c1,
c2, ... , ck)T
that solves the normal equations
XTXv = XTy,
where X is the matrix whose columns are g1, g2, ... , gk.
Let's look at another example.
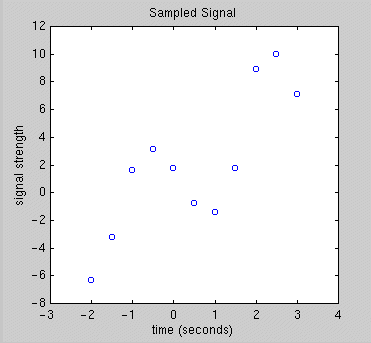
The data below are measurements of the signal output by a small electronic
device. The signal is sampled every half second over the given time
interval. We want to find a sinusoidal model function that provides
a good fit to the observed data.
|
 |
||||||||||||||||||||||||||||
Because of theoretical considerations based on physical properties of such electronic devices, we believe that a likely model function for the given output is a trigonometric polynomial of the form
f(t) = a0 + a1 sin(t) + b1 cos(t) + a2 sin(2t) + b2 cos(2t).
The figure below shows such a candidate function. We want to choose the parameters a0, a1, b1, a2, and b2, to minimize the sum of squares of the residuals, which are shown in the figure. That is, we want the best least squares fit.

are defined in your helper
application worksheet. Solve the normal equations to find the trigonometric
polynomial of best least squares fit.
|
|