|
|
|
|
y = a ebt
to the U.S. population data from Part 1. The standard trick is to linearize the model by taking logs:
ln(y) = ln(a) + b t.
Now we have a model in which the parameters A = ln(a) and b appear linearly. We can fit a least squares line to the data
(T1, ln(Y1) ) ), (T2, ln(Y2) ), ... , (T10, ln(Y10) ).
That is, we fit a least
squares line to the semi-log plot of ln(y) versus t shown below.
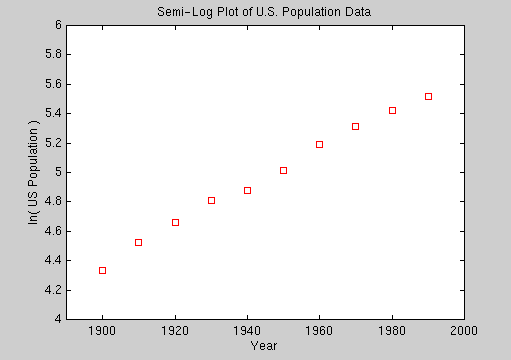
For the U.S. population data, the vectors
y* = ( ln(Y1), ln(Y2), ..., ln(Y10) )T,
t = ( T1, T2, ..., T10 )T ,
Plot the exponential function that you just found together
with a scatter plot of the original U.S. Population data
(not the logarithms). How good is the fit?
Compute the residuals y - p and the sum of squares S of the residuals. Make a residual plot. What do you learn from the plot about the goodness of fit?
Compare the fit of the exponential model to the quadratic model
of Part 1. You should have already computed S
for the the quadratic model.
You should also make a residual plot for the quadratic
model for comparison purposes.
|
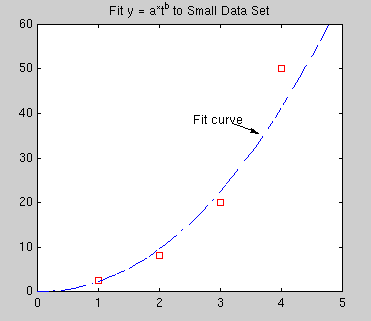 |
||||||||||||||
Above is a small data set. Let's try to fit this data with a power function of the form
by first linearizing the model by taking logs:
ln(y) = ln(a) + b ln(t).
t* = ( ln(T1), ln(T2), ln(T3), ln( T4) )T ,
|
|