Part 1: Example:  Quadratic Fit to U.S. Population Data

U.S. Populations [ Census data] Year Population  (in millions) 1900 75.996 1910 91.972 1920 105.711 1930 122.775 1940 131.669 1950 150.697 1960 179.323 1970 203.185 1980 226.546 1990 248.710

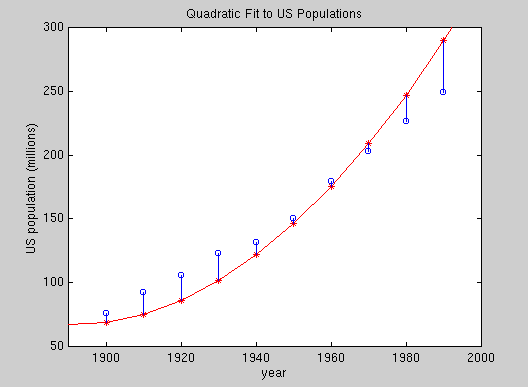
Our model function is a quadratic of the form y = a + b t + c t².  Below, we plot such a quadratic function, along with vertical line segments indicating the deviations or residuals from the data points to the corresponding points on the model curve. As in the "Least Squares" module, our criterion for best fit is that the best choice of quadradic curve should minimize the sum of the squares of the residuals -- hence the name "least squares."

Remark about notation: As in the "Least Squares" module, we will maintain a distinction between vectors and scalars by boldfacing vector names but not boldfacing scalars.

1. Suppose we represent the data points as

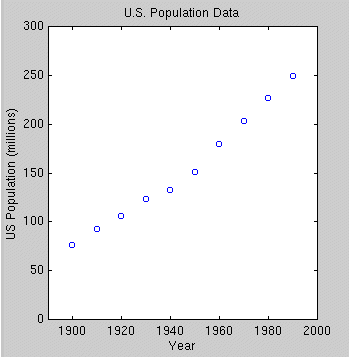
(T₁,Y₁), (T₂,Y₂), ..., (T₁₀,Y₁₀).

Explain why the quantity to be minimized is

[Y₁ - (a + bT₁+ cT₁²)]² + [Y₂ - (a+ bT₂+ cT₂²)]² + ...
+ [Y₁₀ - (a + bT₁₀+ cT₁₀²)]².


 
2. Our least squares problem is to find numbers a, b, and c so as to minimize the distance in R¹⁰ between the vector
   
   
y = (Y₁, Y₂, ..., Y₁₀)^T

and the set of vectors of the form

(a+ bT₁+ cT₁²,  a+ bT₂+ cT₂², ... ,  a + bT₁₀+ cT₁₀²)^T.

Let

t = (T₁, T₂, ..., T₁₀)^T,

t² = (T₁², T₂², ..., T₁₀²)^T

and 1 = (1, 1, ..., 1)^T

be vectors in R¹⁰. Then the set of vectors described two sentences above can also be described as the set of vectors of the form

a 1 + b t + c t²

where a, b, and c are real numbers.  



• Explain why this set is a subspace of R¹⁰. (We call this space the model space.)
  
  
• Explain why the least squares problem is to find the closest vector in the model space to the vector y.

 
3. What are the possible dimensions of the model space? What would it mean if the dimension were something other than 3?
   
   
4. What would it mean if the vector y were in the model space? Do you think that this the case for the U.S. population data? Why or why not?
   
   
5. Let  W = Span(1, t, t²) be the subspace spanned by the three vectors defined in step 2.   If  p = a 1 + b t + c t²  is the projection of y onto W, then explain why we can write
   
   p = Xv,

   where X is the matrix with columns 1, t, and t² and v is the solution vector (a, b, c)^T.
   
   

6. Since p is the projection of y onto the subspace W, we know that y - p is othogonal to the entire subspace W, in particular to vectors 1, t, and t².  Explain why this orthogonality can be expressed as

   X^T(y - p) = 0.

   Show that this implies that v must satisfy the matrix equation

   X^TXv = X^Ty.

   This matrix equation consists of three scalar equations in the three parameters a, b, and c of the best fitting quadratic model.  The equations are known as the normal equations.
   
   

7. In your helper application worksheet, you will find the vectors 1, t, t², and y for the U.S. population data.  Note that time is measured in years since 1900. Form the matrix X and solve the matrix form of the normal equations for the parameters a, b, and c of the best fitting quadratic.
   
   

8. Plot the least squares quadradic that you just found together with a scatter plot of the U.S. population data.  How good is the fit?
   
   

9. Compute the projection p of y onto the subspace W and also compute y - p.  Explain the relationship between these vectors and features of your plot from the previous step.
   
   

10. One common measure of goodness of fit is the sum of the residuals, the least-squares function that we have minimized. Tell why this quantity can be computed as  S = norm(y - p)².  Compute S for the quadratic fit you have found.