Linear Filters, Part 3

Linear Filters

Part 3: Filtering Frequencies Out

In this part, we are going to see how to predict which frequencies are filtered out by a linear filter. We need to recall some facts from the Difference Equations module.

As in Part 1, let S be the set of all doubly-infinite sequences. Then the equation

y_k+n + a₁ y_k+n-1 + .... + a_n-1 y_k+1 + a_n y_k = z_k

describes a linear transformation T: S -> S with T({y_k}) = {z_k} . The null space (or kernel) N of T is the set of solutions of the homogeneous equation

y_k+n + a₁ y_k+n-1 + .... + a_n-1 y_k+1 + a_n y_k = 0.

N is an n-dimensional vector space, and an exponential sequence, y_k = r^k, is in N if and only if

rⁿ + a₁ r^n-1 + ... + a_n-1 r + a_n = 0.

This polynomial equation is called the auxiliary equation or characteristic equation. Its solutions r₁, r₂, ..., are called characteristic roots of the difference equation. If the auxiliary equation has n distinct roots, then these exponential sequences constitute a basis for the null space N of T. Once again, we will consider only situations in which the characteristic roots are distinct. However, we now wish to consider cases where the characteristic roots are complex.

Consider the homogeneous linear difference equation

y_k+2 + y_k = 0.
Construct the auxiliary equation and find the characteristic roots. You should get two imaginary roots r₁ and r₂.
According to what you learned in Part 4 of the Difference Equations module, {r₁^k} and {r₂^k} should be two linearly independent solutions to our linear difference equation. Use your computer algebra system to check that they are both solutions.

However, these are complex solutions, and for the purpose of signal processing we need to know about the real solutions.

Using polar coordinates, write the r₁ and r₂ that you have found as

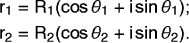
$\begin{align*} r_1 &= R_1 (\cos \theta_1 + i \sin \theta_1);\ r_2 &= R_2 (\cos \theta_2 + i\sin \theta_2).\end{align*}$

A famous law of complex numbers known as de Moivre's Rule then tells us that

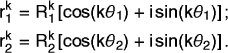
$\begin{align*} r_1^k &= R_1^k (\cos (k \theta_1) + i \sin (k \theta_1));\ r_2^k &= R_2^k (\cos (k \theta_2) + i \sin (k \theta_2)).\end{align*}$

Use this law to rewrite the sequences {r₁^k} and {r₂^k} that solve the difference equation in Step 1.
Prove that if {y_k} is a sequence of complex numbers that solve the homogeneous linear difference equation

y_k+n + a₁ y_k+n-1 + .... + a_n-1 y_k+1 + a_n y_k = 0

then the sequences of real numbers {Re y_k} and {Im y_k} are also solutions to the same linear difference equation. (Remember that the coefficients a_k are all real.)
You can now write four real solutions to the linear difference equation in Step 1, which look like:

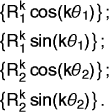
$\begin{align*} & \{R_1^k \cos (k \theta_1)\};\ & \{R_1^k \sin (k \theta_1)\};\ & \{R_2^k \cos (k \theta_{2})\};\ & \{R_2^k \sin (k \theta_{2})\}.\end{align*}$

Use your computer algebra system to verify that these are in fact solutions.
However, we know that the set of solutions to this linear difference equation is 2-dimensional, so some of these solutions must be linearly dependent. Find two of the real solutions above that make a linearly independent set.

You now know how to find the real sequences that are solutions to the homogeneous equation

y_k+n + a₁ y_k+n-1 + .... + a_n-1 y_k+1 + a_n y_k = 0.

If we consider once again the linear filter

y_k+n + a₁ y_k+n-1 + .... + a_n-1 y_k+1 + a_n y_k = z_k

then we can regard the solutions of the homogeneous equation above as the input signals that are taken to zero by the filter; that is, those that are filtered out.

Find a linearly independent set of two signals that are filtered out by the linear filter

y_k+2 + y_k = z_k.
Use the techniques above to find as large a linearly independent set of signals as you can that are filtered out by the linear filter

y_k+4 - y_k+2 + 2 y_k = z_k
from Part 2. Compare your answers to the observations you made there.