Go to CCP Homepage Go to Materials Page Go to Linear Algebra Materials Go to Table of Contents
Go Back One Page Go Forward One Page

Curve Fitting

Part 4:  Pitfalls of Linearization

We saw in Part 3 that some models in which the parameters do not appear linearly can be "linearized" so that the standard least squares fitting methods can be used. In Part 3, we fitted an exponential model to the U.S. population by first taking logs of the y data values. We were fortunate that the linearization trick worked well and we got a good fit.

Linearization is not always an effective method however. Sometimes, the model equation is sufficiently complicated so that no linearization trick exists. For example the logistic model

y = K P0 / ( P0 + (K - P0) exp(-r t) )

is highly non-linear in all three parameters P0, K, and r.  There is no obvious way to use logarithms or algebraic manipulations to "linearize" the problem of doing a logistic fit.

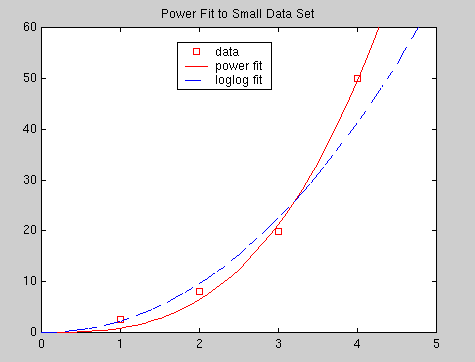
In other cases, even though a linearization can be found, the fit found using the linearization is worse than one could obtain by fitting the model by even trial and error. To illustrate this point, consider again the power-function fit to the small data set that you did in Part 3. By fitting a straight line to the log-log plot of the data, you should have found the corresponding power function

y = 2.225 t2.108,

which yielded the sum of squares of residuals S = 84.3 for the data.

One can easily find a much better fit. The power function

y = 0.848 t2.935

yields a sum of squares of residuals S = 7.20 for the same data. In Part 5, we will show that this power function does, in fact, yield the minimum value of S. In the figure below, the fits of these two power functions are compared. The fit from Part 3 is labeled "log-log fit" and the optimal fit is labeled "power fit".
 


Comparsion plot of power vs. llog fits


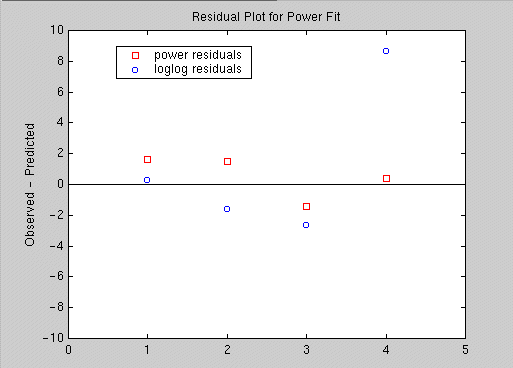
Below, we show a comparison of the residual plots of these two models. The "log-log" model fits the data very poorly at the right end of the plot.
 


Compare residuals of power vs. llog fits


  1. Explain how it can be that the power-function fit we got by fitting the log-log data can be worse than some other power function fit. After all, we did do a least squares fit. The sum of squares S should be minimized, shouldn't it?

  2. Fit an exponential function to the small data set of Part 3 by using the same (semi-log) linearization technique you used in fitting the U.S. population earlier in Part 3. Compute the sum of squares of residuals S for the exponential fit you find. You should get S = 6.81.

  3. Compare your fit from step 2 to the value of S you get for the exponential function

    y = 0.921 e0.999t


    that was simply chosen to pass though the first and last points of the small data set. Show residual plots of both exponential fits together in the same figure. What do you learn from the plot?


Go to CCP Homepage Go to Materials Page Go to Linear Algebra Materials Go to Table of Contents
Go Back One Page Go Forward One Page

modules at math.duke.edu