|
|
|
|
|
|
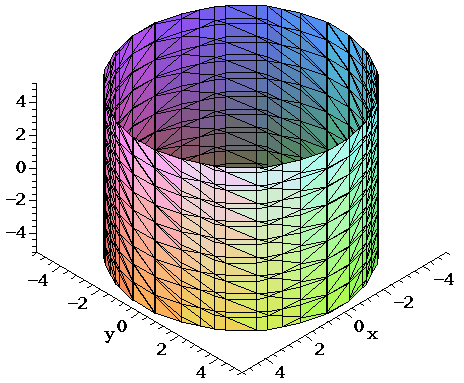
A cylinder is a surface traced out by translation of a plane curve along a straight line in space. For example, the right circular cylinder shown below is the translation of a circle in the xy-plane along a straight line parallel to the z-axis. (The "right" in the name means that the translation is along a line perpendicular to the plane of the "generating circle.")
We can use that description to write an equation for the surface: The "generating circle" in the plane is x2 + y2 =16. If we interpret that equation as having three variables (with 0 coefficient for z), the equation describes every point on the surface.
This idea works for all cylinders that are parallel to one of the coordinate axes. For example, if we translate the parabola y2 = z in the yz-plane along the x-axis, we get the parabolic cylinder defined by the same equation. (Like the previous example, this is a "right" cylinder, but of course it's not a circular cylinder.) The following figure is a graph of this parabolic cylinder.
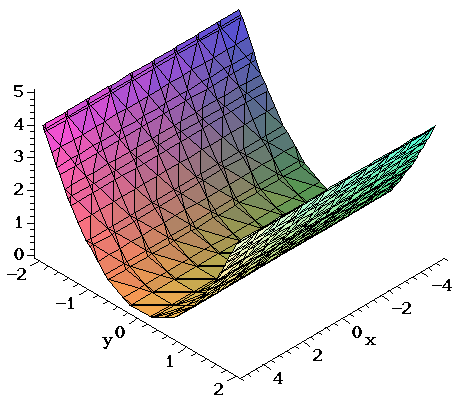
The equations for both the circular and parabolic cylinders are quadratic, so technically these are quadric surfaces. However they are "degenerate" quadrics because each of the equations has a variable with 0 coefficient. As we will see in step 4, not all cylinders are quadric surfaces.
|
|
|
| CCP Home | Materials | Multivariable Calculus | Module Contents | Back | Forward |
modules at math.duke.edu
Copyright
CCP and the author(s), 2001-2002