|
|
|
|
|
|
In Part 1 we saw that, given a continuous function f(x), we may construct a new function F(x) by definite integration of f up to a variable upper limit x:
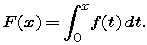
We saw further that F'(x) = f(x) -- that is, F is an antiderivative of f.
Another way to say the same thing is this: If we integrate a function f to a variable upper limit x, and then differentiate the resulting function with respect to x, we get back where we started. In short, differentiation undoes (definite) integration.
In this part, we study the effect of doing the operations in the other order: differentiation first, then integration. The result will be similar to that in Part 1, but subtly different.
As in Part 1, we will continue with the example function
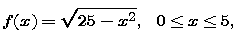
Our reason for selecting this function -- apart from familiarity of its graph -- is that you probably do not know a simple formula for an antiderivative. Nevertheless, we were able to construct an antiderivative function without knowing (or finding) such a formula. Of course, you do know how to differentiate this function -- but we will not immediately make use of that knowledge.
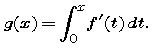
Graph both f ' and g, and explain why the graph of g has the form it has. In particular, why are all the values of g negative?
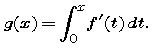
but we don't know anything about f(x) other than the fact that it is continuously differentiable -- i.e., f ' exists and is a continuous function. Write a formula for the relationship between g and f. Use the fact that both of these functions are antiderivatives of f '. Since you don't know values for f, your formula will have to contain the unknown value f(0).
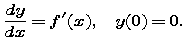
|
|
|
| modules at math.duke.edu | Copyright CCP and the author(s), 1999 |