|
|
|
|
|
|
Many useful functions are naturally described by integration of known functions. Sometimes these newly defined functions turn out to be functions we already know in some other context -- sometimes they are truly new. In this part we define a function F(x) by integrating a given continuous function f(x), and then we study the derivative of the new function F(x).
For our initial example, we start with the function
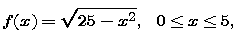
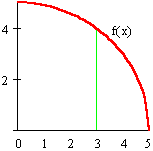
whose graph is a quarter-circle of radius 5:

We define a new function F(x) by setting its value at a positive number x to be the integral of f from 0 to x:
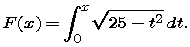
Note that, since x is being used to represent the independent variable for the function F, a different variable t is used for the variable of integration.
What does this function definition mean? Since the definite integral of a positive function f represents area under the graph of f, we may think of F(x) as the area under the graph of f(t) between t = 0 and t = x. We illustrate this in the following figure.
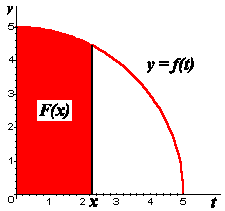
To see the construction of the function F dynamically, click on one of the following animations. But first, please read these instructions.
F(x) animation options: Least smooth (93K), smoother (316K), smoothest (762K).
We turn our attention now first to estimating, then to calculating, the derivative of F(x). For purposes of estimation, we will calculate difference quotients
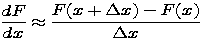
with the difference 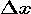 = 0.001. (Any reasonably small value of
= 0.001. (Any reasonably small value of 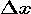 would do -- you are welcome to experiment with other values in your worksheet.)
would do -- you are welcome to experiment with other values in your worksheet.)
Your results in step 3 should strongly suggest a connection between F'(x) and f(x). However, a handful of approximately equal pairs of numbers is not enough to establish equality. We consider now why that apparent equality might actually be true.
First we consider the change in function values of F when x is incremented by 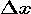 :
:
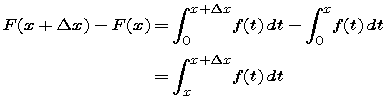
by the definition of F and a property of definite integrals. Thus, the change in F is the area under the graph of f between x and x + 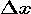 . [Note: We are using implicitly the fact that f(x) is nonnegative when we refer to area. However, the conclusion remains correct for any continuous function if we use the concept of "signed area."]
. [Note: We are using implicitly the fact that f(x) is nonnegative when we refer to area. However, the conclusion remains correct for any continuous function if we use the concept of "signed area."]
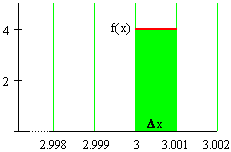
We illustrate the area interpretation of the change in F in the next pair of figures, using x = 3 and 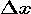 = 0.001. The left figure shows the area under the graph of f between 3 and 3.001 shaded in green. Because the interval is so small, the shaded region looks rather like a line. In the right figure, we have left the vertical scale the same but have greatly expanded the horizontal scale. Again, the area under the graph of f between 3 and 3.001 is shaded in green.
= 0.001. The left figure shows the area under the graph of f between 3 and 3.001 shaded in green. Because the interval is so small, the shaded region looks rather like a line. In the right figure, we have left the vertical scale the same but have greatly expanded the horizontal scale. Again, the area under the graph of f between 3 and 3.001 is shaded in green.
|
|
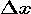 , give a quick estimate of the area under the graph of f over the interval [x, x +
, give a quick estimate of the area under the graph of f over the interval [x, x + 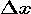 ].
].
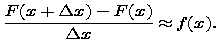
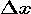 gets smaller, and
gets smaller, and
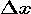 .
.
Explain the following calculation of the instantaneous rate of change of F:
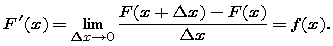
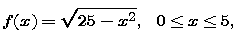
use your helper application to confirm the formula in step 10. That is, ask the computer algebra system for a symbolic formula for F(x). Then ask for the derivative of that formula, and confirm that the result is equivalent to the formula for f(x).
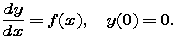
|
|
|
| modules at math.duke.edu | Copyright CCP and the author(s), 1999 |