SIR Model, Part 3

The SIR Model for Spread of Disease

Part 3: Euler's Method for Systems

In Part 2, we displayed solutions of an SIR model without any hint of solution formulas. This suggests the use of a numerical solution method, such as Euler's Method, which we introduced in the Limited Population and Raindrop modules.

Recall the idea of Euler's Method: If we have a "slope formula," i.e., a way to calculate dy/dt at any point (t,y), then we can generate a sequence of y-values,

y₀, y₁, y₂, y₃, ...

by starting from a given y₀, and computing each rise as slope x run. That is,

y_n = y_n-1 + slope_n-1 Delta-t

where Delta-t is a suitably small step size in the time domain.

It really doesn't matter in this calculation if the slope formula happens to depend not just on t and y but on other variables, say x and z -- as long as we know how x and z are related to t and y. If x and z happen to be other dependent variables in a system of differential equations, we can generate values of x and z in the same way.

Of course, for the SIR model, we want the dependent variable names to be s, i, and r. Thus we have three Euler formulas of the form

s_n = s_n-1 + s-slope_n-1 Delta-t,

i_n = i_n-1 + i-slope_n-1 Delta-t,

r_n = r_n-1 + r-slope_n-1 Delta-t,

More specifically, given the SIR equations,

the Euler formulas become

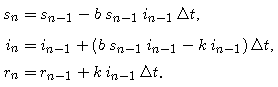
Of course, to calculate something from these formulas, we must have explicit values for b, k, s(0), i(0), r(0), and Delta-t. In this part we explore the adequacy of these formulas for generating solutions of the SIR model. If your helper application has Euler's Method as an option, we will use that rather than construct the formulas from scratch.

Use your helper application's differential equations solver, with the sample values of b = 1/2 and k = 1/3 in your worksheet, to generate graphical solutions of the SIR equations, starting from s(0) = 1, i(0) = 1.27 x 10^-6, and r(0) = 0.

Now generate Euler's Method solutions for the three sectors of the population. Start with a relatively coarse step size of Delta-t = 10 days, and let t range up to 150 days. Superimpose these solutions on the "exact" solutions from Step 1. Do you think the Euler solutions closely track true solutions of the system? Why or why not? What characteristic of Euler's Method causes the approximate solutions to behave the way they do?

Change the step size to 1 day and replot the Euler solutions. Now do they closely track true solutions of the system? Why or why not?

Find a step size for which the Euler solutions appear to closely track true solutions of the system.