Joint work with Simon Levin, Princeton U

Allelopathy in Spatially Distributed Populations

Some strains of E. coli produce a toxic substance, known as colicins, that kill or inhibit the growth of competing bacteria of different genotypes, a process known generally as allelopathy . The strains that produce colicin are immune to its action. Most theoretical studies of the competition of colicin producing and colicin sensitive bacteria assume that the population is homogeneously mixing to arrive at ordinary differential equations (ODE) describing their dynamics. (See Chao and B.R. Levin (1981) or Frank (1994).) If we let u be the density of the colicin producing strain and v be the density of the colicin sensity strain then we typically have

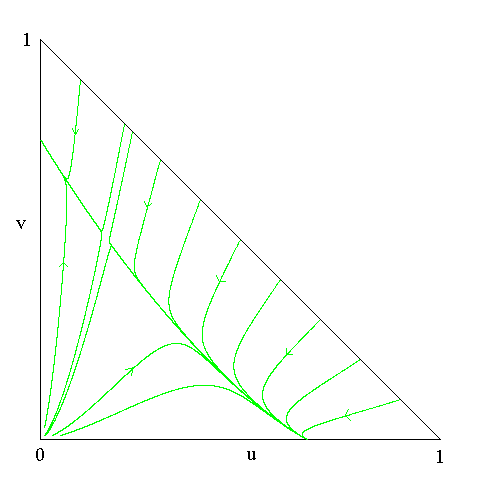
The implication of this picture is that colicin production and colicin non-production are each evolutionarily stable strategies, i.e., a pure population of one type in its equilibrium cannot be invaded by the other type. The last conclusion changes if we look at the situation through the eyes of a spatial model. In our model each point in the square lattice can be in state 0 = vacant, 1 = occupied by a colicin producer, 2 = occupied by a colicin sensitive bacterium. Each type is born at empty sites at a rate proportional to the fraction of the four nearest neighbors occupied by that type. The colicin producing strain dies at a constant rate 1 while the colicin sensitive dies at rate 1 plus c times the fraction of colicin producing neighbors. Because of the last situation it is natural to assume that the birth rates for the two strains satisfy b1 < b2. The next four pictures show the evolution of the system with b1=3, b2=4, c=3 starting from 1% sites of type 1 (red sites) and 50% of type 2 (green sites).

Time 50 Time 300

Time 600 Time 900

The situation described here is an instance of Case 2 of Durrett and Levin (1994). The ODE has two attracting fixed points and predicts that the winner of the competition depends on the initial densities. In contrast, for the spatial model there is a stronger type that takes over the system whenever it starts with a positive density. To be precise we conjecture that the stronger type always wins if there are infinitely many individuals of that type present in the initial configuration. Here, by ``wins'' we mean that the probability a given site x will be occupied by the weaker type converges to 0.

Empirically, the stronger type can be characterized by the behavior of the system starting from all 2's on half plane x < 0 and all 1's on the other half. 2's win if the boundary moves to the right at a linear rate, 1's win if the boundary moves to the left, and coexistence is never possible.

The last two paragraphs describe the behavior of "Case 2" systems. Even proving rigorously that the interface moves at a linear rate with a well defined speed seems to be an impossibly difficulty problem. However, the idea that interface speeds identify the stronger equilibrium has been used by Durrett and Neuhauser (1994) and Durrett and Swindle (1994) to prove results for particle systems with fast stirring. However, neither that assumption nor the alternative of long range interactions seems appropriate in this context.

Durrett, R. and S.A. Levin (1994) The importance of being discrete (and spatial). Theoret. Pop. Biol. 46 , 363--394

Durrett, R. and C. Neuhauser (1994) Particle systems and reaction diffusion equations. Ann. Probab. 22 , 289--333

Durrett, R., and G. Swindle (1994) Coexistence results for catalysts. Prob. Th. Rel. Fields 98, 489--515

Frank, S.A. (1994) Spatial polymorphism of bacteriocins and other allelopathic traits. Evolutionary Ecology