The Broken Stick Problem

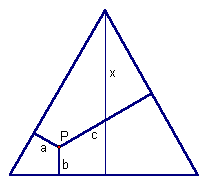
This altitude theorem can be used to find an answer to a famous probability problem:  If a stick of length x is broken into three pieces, what is the probability that the three pieces can be used to construct a triangle?

This problem is more difficult then it may originally seem because the sum of the two smaller sides of the triangle must be greater than the third side.  For instance, if the stick is broken into pieces of 2 inches, 3 inches, and 10 inches it will be impossible to construct a triangle.

Given an equilateral triangle with altitude x, it is possible to use geometry to solve the problem.

Any point within the triangle can represent how the stick is broken into three pieces.  For instance, if point P is selected, that represents that the stick is being broken into pieces with length a, b, and c.  By the altitude theorem, it is known that a + b + c = x

In this example it would not be possible to make a triangle, because a + b < c.

To find the probability that the two smaller sides will sum to be larger than the third side it is helpful to divide the equilateral triangle into four smaller equilateral triangles, by connecting the midpoints of the sides.

As long as point P is selected in the middle triangle, it will be possible to create a triangle from the three pieces.  (Why?)  The probability that randomly selected P is in the middle triangle is 1/4 so the probability that a triangle can be created from breaking a stick into three pieces is 1/4.