Maple Tool2.mws

Maple Tool 2

This tool is designed for use with Checkpoint 3 in Section 7.1.

Part (a)
 f1:=x->sin(x);
plot(f1(x),x=-2*Pi..2*Pi);

f1 := proc (x) options operator, arrow; sin(x) end proc

[Maple Plot]

Part (b)
 f2:=x->sin(1/x);
plot(f2(x),x=0..1);

f2 := proc (x) options operator, arrow; sin(1/x) end proc

[Maple Plot]

Part (c)

We calculate this in two parts in order to see the graph of the whole function.  Maple has a problem with fractional powers of negative numbers, as illustrated in PlotA, where we plot from -1 to 1 but see the graph only from 0 to 1.  We get the other half of the graph by using symmetry: 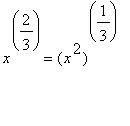  x^(2/3) = (x^2)^(1/3) , so f3  has a value at every x  other than 0, and f3(-x) = f3(x) , which means f3  is an even function.

  with(plots):
f3:=x->1/3*x^(-2/3);
PlotA:=plot(f3(x),x=-1..1, view=[-1..1,-2..2]):%;
PlotB:=plot(f3(-x),x=-1..0, view=[-1..1,-2..2]):%;
display(PlotA, PlotB); 

Warning, the name changecoords has been redefined

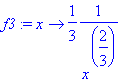
f3 := proc (x) options operator, arrow; 1/3*1/(x^(2/3)) end proc

[Maple Plot]

[Maple Plot]

[Maple Plot]

Part (d)

As in part (c), there are numbers not in the domain of the function, in this case x = sqrt(2)  and x = -sqrt(2) .  We can construct the graph in three parts and display them together.
 f4:=x->(x^2+1)/(x^2-2);
PlotA:=plot(f4(x),x=-3..-sqrt(2),  view=[-3..3, -10..10]):
PlotB:=plot(f4(x),x=-sqrt(2)..sqrt(2),  view=[-3..3, -10..10]):
PlotC:=plot(f4(x),x=sqrt(2)..3,  view=[-3..3, -10..10]):
display(PlotA, PlotB, PlotC);

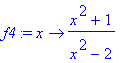
f4 := proc (x) options operator, arrow; (x^2+1)/(x^2-2) end proc

[Maple Plot]

>   

>