|
|
|
|
|
|
Among the simplest differential equations are those of the form
i.e., first-order differential equations where the right-hand side has no explicit dependence on the dependent variable Y. For such an equation, obtaining a general description of the solutions is the same as finding all antiderivatives of f, i.e., the same as calculating an indefinite integral. So, for example, the solutions of
constitute the family of functions Y of the form
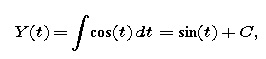
where C can be any constant. More generally, finding symbolic descriptions of solutions of first-order differential equations comes down to calculating one or more integrals.
We describe here a method for calculating symbolic descriptions of solutions for a large class of differential equations -- those that can be written in the form
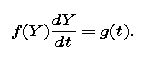
Such differential equations are said to be separable. For example, each of the following differential equations is separable:
dY/dt = Y2
dY/dt = Y(t + 1)
A first example
Before we describe the solution procedure in general, let's look at a simple case,
You probably know that this represents exponential growth or decay depending on whether k is positive or negative and that the family of solutions is
where C can be any real constant. However, let's forget that we know this and rediscover this description.
In the discussion, we will use the fact that initial value problems for this differential equation have unique solutions. In particular, since the constant function zero is a solution, any different solution is never zero. Indeed, suppose Y is a solution of the differential equation and Y(t0) is zero. Then, Y is a solution of the initial value problem
But, the constant zero function is also a solution of the initial value problem
Since there is only one solution of the initial value problem, Y must be the constant zero function.
Thus, we only need to describe solutions that are never zero. Suppose that Y is such a nonzero solution of the differential equation dY/dt = kY. Then,
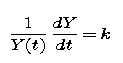
for all t. Think of the left-hand side of this equation as the result of a chain rule differentiation
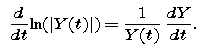
We may also write the right-hand side as a derivative
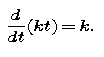
Using these identifications, Y must satisfy

for all t. Since two functions have the same derivative for all t exactly when they differ by a constant, we must have
for some constant c and all t. Now exponentiating both sides of this equation, we obtain
Since Y(t) is either always positive or always negative, either Y(t) = ecekt for all t or Y(t) = -ecekt for all t. If we let C be either ec or -ec as appropriate, then Y must have the form
Letting C be any nonzero constant, we describe all the nonzero solutions of the differential equation. If we allow C to be zero, we also pick up the constant zero solution in our description.
A mnemonic device
Now we will repeat this calculation in a mnemonic form that makes the steps easy to remember. First, rewrite the differential equation in the form
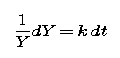
Notice that we have "separated the variables." Now formally integrate both sides. (This is the Chain Rule step in the original calculation.) We obtain
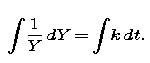
Carrying out the indicated integrations, we have
Combining the two constants, we have
The rest of the calculation is as before.
The general method
In general, if the differential equation is separable, we can separate the variables
Then, if we can evaluate the integrals

we reduce the problem from one of calculus to one of algebra -- solving for Y(t).
A second example
Let's try this out with the differential equation dY/dt = 5Y2. Certainly one solution of this differential equation is the constant zero function.
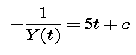
for all t.
show that
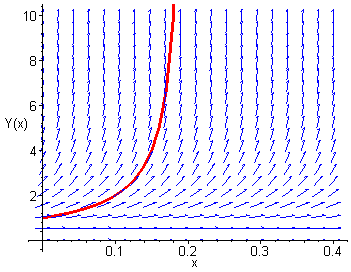
A third example
As a final example of this method of determining symbolic solutions, we'll look at the differential equation
Note that this is our rumor-spreading differential equation from Part 1 with k and M both set equal to 2.
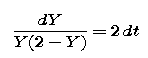
Integrate both sides to show that Y must satisfy

and show that the description in Step 6 agrees with the computer algebra system description.
|
|
|
| modules at math.duke.edu | Copyright CCP and the author(s), 1999 |