|
|
|
|
|
|
The second type of multiplication for vectors in space is called the cross or vector product. As the second name implies, the result of cross-product multiplication of two vectors is another vector. This new vector is perpendicular to the plane in which the first two vectors lie. Note that there are two possible directions in which the cross product of two vectors may point. This potential problem is solved by the right-hand rule, as we will explain. We will use the notation cross(v,w) to denote the cross product of two vectors. It is also written v x w -- hence the name "cross product."
We begin by observing that if v = w, then these "two" vectors are one, and there is no single plane determined by them. Thus, we require that cross(v,v) = 0, the zero vector, so the result is perpendicular to every plane that might contain v.
Next we define the cross product for pairs of the basic unit vectors i, j, and k. Each of these is perpendicular to the plane of the other two, so we can define cross(i, j) to be k -- or maybe -k. Let's see which makes sense. The usual convention for coordinates in space is the right-hand rule, as illustrated in the following figure:

That is, if we follow the direction of the fingers to go from the x-axis to the y-axis, then the thumb points in the direction of the z-axis. The unit vectors i, j, and k of course point in these same directions. Thus, if we adopt the right-hand rule for cross products as well, then we want cross(i, j) to be k, as illustrated in the following picture:
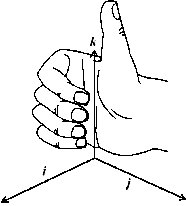
| cross | i | j | k |
| i | 0 | k | -j |
| j | |||
| k |
Now we extend the cross product to arbitrary vectors in space by requiring that it satisfy the ordinary distributive rules of algebra. Thus, we compute the cross product of v = (a,b,c) = ai + bj + ck and w = (d,e,f) = di + ej + fk as
cross(v,w) = ad(i x i) + ae(i x j) + af(i x k)
+ bd(j x i) + be(j x j) + bf(j x k)
+ cd(k x i) + ce(k x j) + cf(k x k)
cross(v,w) = (bf-ce, cd-af, ae-bd)
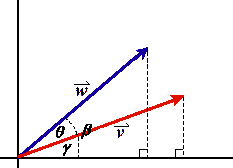
This cross product satisfies the right-hand rule in general, as illustrated in the following figure. (You will confirm this algebraically in step 4 below.) However, it is not immediately obvious how the length of cross(v,w) is related to the vectors v and w.

Geometrically, the cross product tells us something about the area of the parallelogram formed by v and w. The figure below shows this parallelogram. For simplicity, we suppose that v and w both lie in the xy-plane.
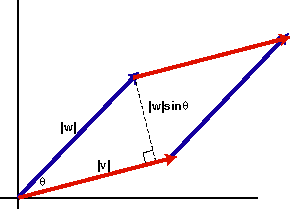
| ![]() |.
|.
![]()
to relate |cross(v,w)| to the angle ![]() between the two vectors. Finally, show that |cross(v,w)| is the area
found in step 6.
between the two vectors. Finally, show that |cross(v,w)| is the area
found in step 6.
Summary of this section
The cross product of v and
w is a vector that is perpendicular to both v and w and
has length equal to |v| |w| sin ![]() ,
where
,
where ![]() is the smaller of the two
angles between v and w. In general, there are two vectors that
satisfy these conditions -- the one we want is given by the Right Hand Rule.
The length of the cross product is also the area of the parallelogram determined
by the two vectors.
is the smaller of the two
angles between v and w. In general, there are two vectors that
satisfy these conditions -- the one we want is given by the Right Hand Rule.
The length of the cross product is also the area of the parallelogram determined
by the two vectors.
This shows that the cross product tells us something geometrically significant about the vectors' relationship in the plane in which they lie. This fact will be important when we study surfaces, since surfaces look much like planes when viewed at small scales. It is also important for the study of flux lines for electric and magnetic fields.
|
|
|
| CCP Home | Materials | Multivariable Calculus | Module Contents | Back | Forward |
modules at math.duke.edu
Copyright
CCP and the author(s), 2001-2002