Green's Theorem
and the Planimeter
Part 1: Iterated Integrals and Line Integrals
The first few questions in this part
are designed to help you review iterated integrals and, in particular, to review
using a computer algebra system (CAS) to evaluate these integrals. Your worksheet
contains the commands to evaluate the two integrals described in the following
figures.
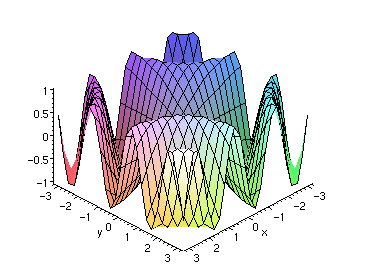 |
 |
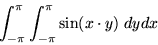 |
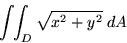
where D is the unit disk centered at the origin. |
If you find this material or the computer
commands unfamiliar, you might consider reviewing the topic of iterated integrals
by working through the modules Double Integrals
I and/or Double Integrals II.
- Use the command in your worksheet
to evaluate the integral
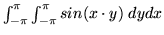 . Does your
CAS have any difficulty finding a numerical value for the integral? If so,
what do you attribute this to?
. Does your
CAS have any difficulty finding a numerical value for the integral? If so,
what do you attribute this to?
- Plot the graph of the function
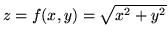 , and use the geometry of this graph to evaluate
the integral
, and use the geometry of this graph to evaluate
the integral
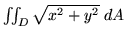 where D is the unit disk centered
at the origin.
where D is the unit disk centered
at the origin.
- Use your CAS to evaluate the integral
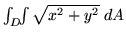 in step 2.
in step 2.
- Set up and evaluate the integral:
where 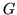 is the region enclosed by the ellipse
is the region enclosed by the ellipse
Next, you will practice setting
up and evaluating line integrals. If
a curve C in the plane is parametrized by a function
![$\gamma: [a,b] \rightarrow$](img12.gif) R
R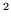 , say
, say
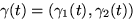 ,
then
,
then
- Use your CAS to evaluate the line
integral
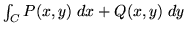 when
when 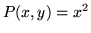 ,
, 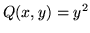 , and C is the boundary of the square
with vertices at (0,0), (1,0), (1,1), and (0,1), traced out in a counter-clockwise
direction.
, and C is the boundary of the square
with vertices at (0,0), (1,0), (1,1), and (0,1), traced out in a counter-clockwise
direction.
- How can you express the line integral
in step 5 as a sum of four simple, one-dimensional definite integrals? How
can this be used to explain the result of your calculation above?
- Set up and evaluate the integral
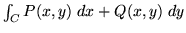 when
when
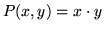 ,
, 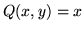 , and C is the boundary of the circle (x - 1)2 + (y - 1)2 = 1,
traced out in a counter-clockwise direction.
, and C is the boundary of the circle (x - 1)2 + (y - 1)2 = 1,
traced out in a counter-clockwise direction.
Next, you will set up and evaluate
some iterated integrals and some line integrals from scratch. Note that you
can save a lot of typing in your worksheet by copying, pasting, and editing.
- Set up and evaluate the following
line integrals, where C is the square with vertices at (0,0), (1,0),
(1,1) and (0,1), traced out in a counter-clockwise direction.
- Set up and evaluate the following
iterated integrals, where D is the interior of the square in step 8.
- Set up and evaluate the following
line integrals, where C is the circle (x - 1)2 + (y - 1)2 = 1,
traced out in a counter-clockwise direction.
- Set up and evaluate the following
iterated integrals, where D is the interior of the circle in step 10.
- What relationships have you noticed
between the values of the iterated integrals and the values of the line integrals?
Summarize the patterns that you have noticed as a conjecture about how the
values of line integrals and iterated integrals may be related.


![]() R
R![]() , say
, say
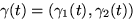 ,
then
,
then