Taylor Polynomials I, Part 2

Taylor Polynomials I

Part 2: Polynomial Approximations to e^x

In Part 1 we saw that a polynomial could be completely determined by its value and the values of its derivatives at x = 0. Further, we found that, as we added terms of higher degree (with the appropriate coefficients), our approximation to the "target" polynomial improved in the sense that the two functions appeared to match over a wider domain centered at 0. In this part we extend this idea to approximations of a nonpolynomial function. Thus, we don't expect to get an exact fit in five steps -- or ever.

Why do we want to do this for a familiar function such as the exponential function? Well, even though e^x is a button on your calculator (and a simple command in your computer algebra system), the way in which its values are computed may still be a mystery. Values of a polynomial function require nothing more than arithmetic, at which your calculator and computer excel. This is not exactly what's going on in your calculator, but in principle it could be. More importantly, the idea of polynomial approximation is very powerful in later work, and it makes sense to study it first in the context of familiar functions.

How do we know that the exponential function e^x is not a polynomial? State at least one property of this function that could not be a property of any polynomial.

Before we start on approximation of the exponential function, we review some notation -- in case this is not already familiar: In part 1 you encountered products of consecutive positive integers, such as 1 x 2, 1 x 2 x 3, 1 x 2 x 3 x 4. These were the result of successive differentiations using the power rule. The product of the first k positive integers, 1 x 2 x ... x k, is called k factorial and is denoted k!. For completeness' sake, we assign the value 1 to such a product with only one factor or with zero factors. Thus, 1! = 1 and 0! = 1.

Using the factorial notation, we can write the result from Part 1 in the following way: The k-th coefficient of an n-th degree polynomial

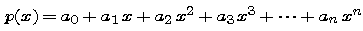
is determined by the formula

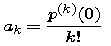
for each k from 0 through n. [Note that we defined 0! and 1! in the right way to make this statement true for those first two cases. In particular, you should read p⁽⁰⁾ as meaning p itself.]

The significance of this formula is that coefficients determined this way can be computed for any function for which the derivative values at 0 are known for every k. More specifically, if f(x) is any function that can be differentiated at least n times, then the numbers

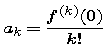
are called the Taylor coefficients of f, and the polynomial

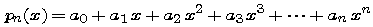
is called the n-th degree Taylor polynomial of f.

For the case of the exponential function, f(x) = e^x, the numbers f(0), f'(0), f''(0), and so on, are not difficult to compute. Make a list of these numbers. You may quit when the pattern in the list is clear.
List the first five Taylor coefficients for the exponential function, i.e., those for k = 0 through 4. Enter these numbers in your worksheet as a₀, a₁, ..., a₄.
Your worksheet contains definitions for the first five Taylor polynomials for e^x. For each polynomial p_n(x),
- plot p_n(x) and e^x together;
- plot the error function, e^x - p_n(x);
- describe the extent to which p_n(x) does and does not approximate e^x.
Assume you are locked in a room with only pencil and paper. You will not be released until you calculate a value of e^5/4 to within 0.01. Extend your calculations in step 4 (if necessary) to find a way to do the calculation, and write out the calculation in your report. You may use your computer algebra system (or a calculator) to do the arithmetic, but it should be arithmetic that you could do by hand if you had to. Use your CAS to check your answer.

Taylor Polynomials I

Part 2: Polynomial Approximations to ex

Part 2: Polynomial Approximations to e^x