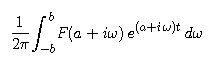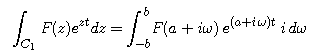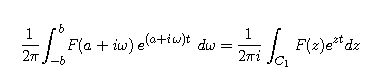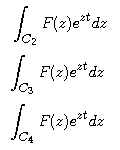The Inverse Laplace Transform
Part 2: An Application of the Residue Theorem
Now let's look more closely at the integrals
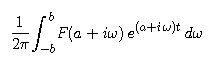
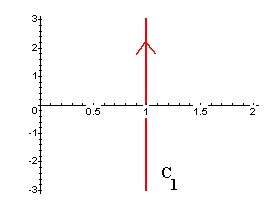
Let Z(omega) = a + i omega for omega between -b and b be a parametric representation for the curve C1. We sketch below an example of C1 with a = 1 and b = 3.
Graph of C1
- Use this parametric representation
to explain why we may write the line integral of F(z) exp(zt)
over the curve C1 as
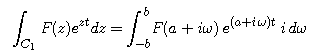
- Explain why we may represent
the integral in the limit representation of f(t) as
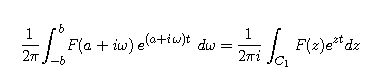
- Now let's concentrate on this
complex function F(z) exp(zt). Find the isolated singularities
of this function, and calculate the residue at each singularity.
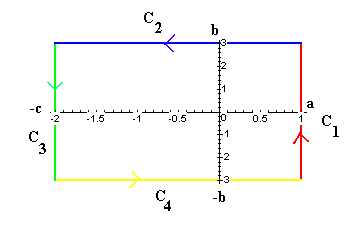
- Next, we'll make C1
part of a rectangular path C that encloses the singularities of F(z) exp(zt)
by adding three additional line segments C2, C3,
and C4 as indicated below.
The Closed Curve C
Use the Residue Theorem to determine
the value of the line integral of F(z) exp(zt) over the closed
curve C. Then, divide this result by 2 pi i and simplify.
Compare this to f(t) for positive t.
- Explain why the result in Step
4 would follow from the fact that, as b and c approach infinity
(leaving a fixed), the limiting value is 0 for each of the following
integrals:
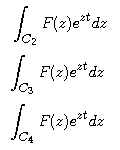
- We will not give a formal proof
of the limits in Step 5. However, check the sizes of the integrals in Step
5 for t = 1, a = 1, and b = c = n for n = 10,
20, and 100.