|
|
|
|
|
|
Our mathematical model describing the spread of the rumor consists of two parts. The first is the differential equation
This second condition is called an initial condition -- the value of dependent variable (in this case S) at the first value of the independent variable (in this case t) under consideration. A differential equation together with an initial condition is called an initial value problem. The implied "problem" is to find a function that satisfies both conditions.
We need to discuss the term "solution." A solution to a differential equation is a function that satisfies the relation for all values of the independent variable under consideration. For example, Y(t) = exp(t) is a solution of the differential equation
The function Y(t) = 3 exp(t) is another solution to this differential equation.
A solution to an initial value problem is a solution to the differential equation that also satisfies the initial condition. So, Y(t) = exp(t) is a solution to the initial value problem
but, Y(t) = 3 exp(t) is not.
One can find a symbolic description for the solution of the initial value problem
Here is such a description:
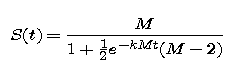
For now, we will not discuss how you could find such a solution. Rather, we will just verify that it works.
You may have to simplify your expressions for the two sides of the differential equation to show they are the same.
| Function | Initial Value Problem | |
| a) | Y(t) = 4 exp(t) - t - 1 | dY/dt = t + Y, Y(0) = -1 |
| b) | Y(t) = 1/(t - 1) | dY/dt = Y2, Y(0) = -1 |
A differential equation usually has infinitely many solutions. This should not be surprising when we realize that finding the family of all antideriavtives for a function f is the same as finding all solutions Y to the differential equation dY/dt = f(t). Indeed, a procedure for finding all solutions of a first-order differential equation usually involves an antidifferentiation step and so the introduction of an arbitrary constant.
|
|
|
| modules at math.duke.edu | Copyright CCP and the author(s), 1999 |