Vectors, Part 3

Vectors in Two and Three Dimensions

Part 3: Vector-Valued Functions and their Derivatives

We define a new type of function, called a vector-valued function, that maps a domain value t to values for each of the coordinates x and y of a vector. One such function is t --> (t, t²), which we denote r(t) = (t, t²).

What is the familiar curve in the plane described by the vector-valued function r(t) = (t, t²)?
Let r(t) = (t², t³). List some of the vectors plotted by this function. How does the curve represented by this function compare to the curve in step 1?
Let r(t) = (cos(t), sin(t)). What shape does this function trace as t varies from 0 to ?

A curve written in this way is also said to be parameterized, and its coordinates are usually written as functions of t by expressing the points on the curve (x,y) as (x(t),y(t)).

How should we differentiate a vector-valued function? Using the definition of the derivative with a vector-valued function r(t) = (x(t), y(t)), we get

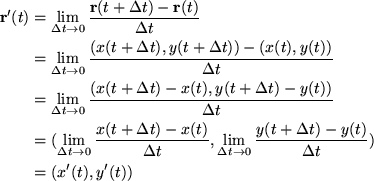
So we only need to compute the derivatives of the coordinate functions. The result of this operation is another coordinate pair -- in other words, the derivative of a vector-valued function is again a vector-valued function. This new function, r^'(t), gives a vector for each value of t that is a tangent vector to the curve at that point. A tangent vector to a curve points in the direction of the familiar tangent line and (by convention) has its base at the point of tangency on the curve instead of at the origin.

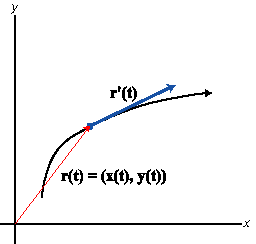
Compute the tangent vector for the function r(t) = (cos(t), sin(t)) at the points (0,1), (1,0), (0,-1) and (-1,0). In what directions do these tangent vectors point? What does this tell you about the parameterization of the curve?

Plot the curve r(t) = (t², t³), and superimpose plots of the velocity (tangent) vectors at t = 1.3 and at t = -1.3. What do you observe about these two vectors? Explain your observation.

An alternate notation for a vector-valued function is r(t) = x(t)i + y(t)j, which expresses the points on the curve as vector sums of the basic vectors i and j. In this notation, the derivative vector of the vector-valued function r(t) = x(t)i + y(t)j is r'(t) = x^'(t)i + y^'(t)j.

Illustrate this by calculating the derivative of the vector-valued function r(t) = (t^3/2)i + cos(2t)j. Plot both r(t) and r'(t) for 0 < t < 8.

On your plot of r(t), superimpose a velocity vector at t = 2.