Surfaces, Part 6

Surfaces and Contour Plots

Part 6: Contour Lines

A contour line (also known as a level curve) for a given surface is the curve of intersection of the surface with a horizontal plane, z = c. A representative collection of contour lines, projected onto the xy-plane, is a contour map or contour plot of the surface.

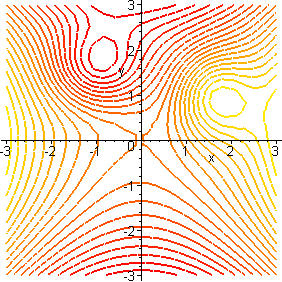
In particular, if the surface is the graph of a function of two variables, say z = f(x,y), then the contours are defined implicitly by equations of the form f(x,y) = c, z = c. The projections into the xy-plane that make up the contour map are defined by f(x,y) = c, z = 0, again for a representative collection of constants c. In the following figure, we show a conventional plot of a function graph on the left and the corresponding contour map on the right. In this map, colors are used to show different elevations, lighter colors at the higher elevations.

Make sure you understand how the contour map represents the function in the figure above. How can you tell from the contour map where there is a "peak" on the surface? a "valley"? a "saddle point"? [A saddle point is a level spot from which you can go down in some direction and up in some other direction.] Give approximate xy-coordinates for each of these three features.

Write down the equations of level curves for f(x,y) = x² + y² for four values of c. Plot this surface and these level curves in your worksheet. If your computer algebra system has a contour option, use it to draw contour lines both on the surface and projected into the xy-plane.

Contour plots are used extensively in geography to indicate the height of the ground above a point on a map. Such maps are called topographical maps. The following figure is an example.

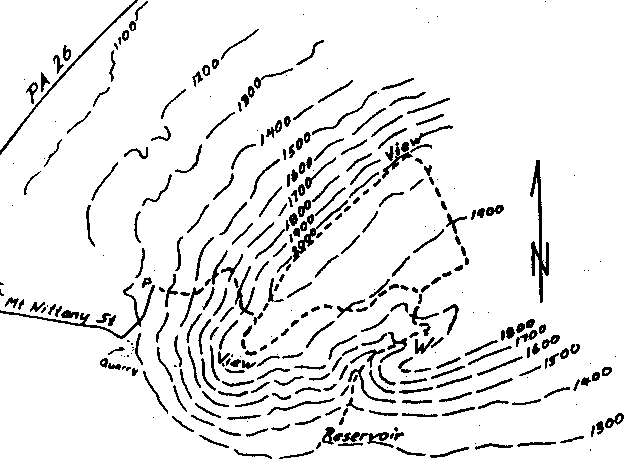
Identify a mountain top in the topographical map shown in the figure above. How can you use contours to be sure of this? How can you distinguish between relatively steep places on the mountain slope from not-so-steep places?

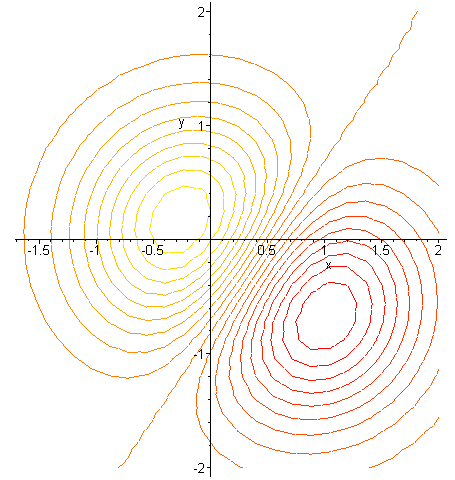
The figure below shows a contour plot of a mathematical function. As in our first example, the lighter contours represent higher elevations. Make a sketch of the surface on paper, as best you can. Then use the commands in your worksheet to plot the function from which this map was made. How well did you read the map?
In your worksheet make a contour plot for the function f(x,y) = 3 - x²- 2y^2,identifying at least four level curves. What are the shapes of these level curves?

Make a contour plot for the Cobb-Douglas function f(x,y) = over 0 < x < 2, 0 < y < 2^,identifying at least four level curves. What are the shapes of these level curves? How do you know?