Parametric Surfaces, Part 2

Parametric Representations of Surfaces

Part 2: Local Change-in-Area Factors

It is often useful to convert from one set of parameters to another. This conversion is called a change of coordinates and can be expressed as a pair of functions from one set of parameters, or coordinates, to the other set.

Let R be the region in the uv-plane defined by and . (See the figure at the right.) Let x(u,v) = u + v and y(u,v) = u - v. Sketch the region S in the xy-plane described by the new coordinate parameters under this change of coordinates. [Hint: Consider separately the boundaries u = 1, u = -1, v = 1, v = -1. In each case, you get a parametric representation for one of the boundaries of S.] How is the area of S related to the area of R?

Let f(x,y) = xy. Set g(u,v) = f(x(u,v),y(u,v)), where the change of coordinates is the one defined in step 1. Compare the graphs of f(x,y) and g(u,v) by plotting them in your worksheet. Are they the same? What are the ranges for x and y?

How do your answers from parts 1 and 2 change if you change the coordinate functions to x(u,v) = u + 2v and y(u,v) = u - 2v?

We have already seen some useful changes of variables, for example the change from Cartesian to polar coordinates in the plane. In particular, this transformation is often useful for simplifying certain integrals.

Compute the double integral

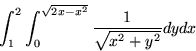first using the given Cartesian variables, and then using polar coordinates in the plane. Plot the domain over which the integration is being carried out.

In the shift from Cartesian to polar coordinates in double integrals, we see that dx dy becomes r dr d, but where does the "r" come from? In deriving our integral formulas, as we subdivided the domain with a polar grid, we had to "scale" each little region by its distance from the origin, so this is our local change-in-area factor for the Cartesian-to-polar transformation. It corresponds in some way to the change of variables

x(r,) = r cos ,
y(r,) = r sin .

In the Cartesian-to-polar case, we could solve the scale problem by elementary geometry. Our task now is to relate this to the algebra of coordinate changes so we can find the local change-in-area factor, no matter what the transformation is.

We have a hint about what we are looking for: the factor used to compute the length of a curve for a parametric representation r(t) = (x(t),y(t)) of a curve C in the xy-plane. For that case, we identified |r'(t)| as the local change-in-length factor that accounts for the stretching and compression done by the function r. We then found the length of the curve for as

For curves, we were able to identify the change-in-length factor because a curve is locally linear. For surfaces, we will obtain the local change-in-area factor using the fact that the surface is locally planar. We consider first the case where the transformation is literally in the plane (as in polar to Cartesian coordinates), and then we extend this to parameterization of a surface, for which two coordinates (parameters) are being transformed into space.

Here is a generic transformation of coordinates in the plane:

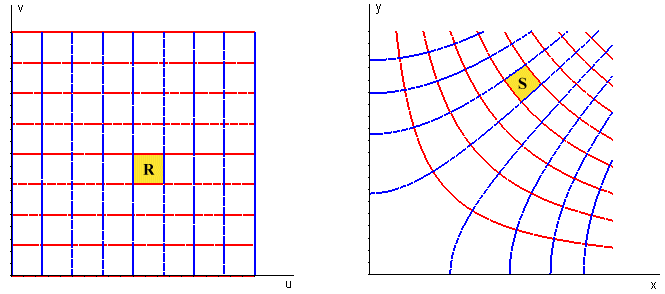
The left figure shows a coordinate grid in the (u,v) plane, with the curves u = constant in blue and the curves v = constant in red. Suppose the transformation formulas into the (x,y) plane are x = x(u,v) and y = y(u,v). Then a blue curve, say u = c, is transformed in the right figure to a blue curve parameterized by (x(c,v),y(c,v)). Similarly, a red curve, say v = k, is transformed in the right figure to a red curve parameterized by (x(u,k),y(u,k)). In the process, a typical coordinate rectangle R in the (u,v) plane is transformed into a "curvilinear rectangle" S in the (x,y) plane. The boundaries of S are formed by the parameterized curves.

Here is a closer look at R and S:

The local change-in-area factor is the ratio of the area of S to the area of R -- that is, the factor by which the area grows or shrinks under the transformation. We can calculate the area of S approximately as the area of the parallelogram determined by the two vectors shown on the right. These are tangent vectors to the parameterized curves, and we know how to calculate tangent vectors as "velocities" -- the "speed" (i.e., magnitude of the velocity vector) is the local change-of-length factor for a parameterized curve. Since each type of curve results from holding one of the variables constant, the relevant derivatives are the partial derivatives of x and y with respect to u and v. Specifically, the tangent vectors are given by

t_u = x_u(u,v) i + y_u(u,v) j,
t_v = x_v(u,v) i + y_v(u,v) j.

These vectors are scaled by the grid spacings du and dv, respectively, to get the vectors on the right that approximate the curve segments in the xy-plane. We calculate the approximate area of S as

|t_u x t_v| du dv,

where now we are thinking of the planar vectors as being in space, so the cross product is in the k direction. Since the area of R is du dv, the length of the cross product is the local change-in-area factor.

Show that, in general, the local change-in-area factor is |x_u(u,v)y_v(u,v) - x_v(u,v)y_u(u,v)|. [Note: This expression is called the Jacobian of the coordinate transformation.]

Show that the polar coordinate change-in-area factor is r. What is the image in the xy-plane of the coordinate rectangle [0,1] x [0,2] in the r-plane? How is the area of this image related to the area of the coordinate rectangle?

Calculate the local change-in-area factor for the transformation x(u,v) = u + v, y(u,v) = u - v in step 1. How is this related to your answer in step 1?

Here's an easy way to calculate the area of an ellipse with semi-major axis a and semi-minor axis b. Parameterize the ellipse as x = a cos , y = b sin . This ellipse is the image of another curve in the uv-plane under the transformation x = au, y = bv. You already know the area enclosed by that other curve, and you can show that the Jacobian is constant. Complete the argument to find the standard formula for area of an ellipse.