|
|
|
|
To create a mathematical model of
the planimeter, you need to describe how the wheel on the moving end of the
planimeter turns. This is because all the planimeter records is the number of
rotations that the wheel has completed. One way to represent this is to define
a vector field in which the vector located at a point 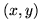 gives the direction that the wheel is rolling in when the planimeter
passes over the point
gives the direction that the wheel is rolling in when the planimeter
passes over the point 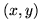 . We show part of this vector field in the following figure.
. We show part of this vector field in the following figure.

The applet below shows the planimeter and the part of the vector field that is nearest the spinning wheel of the planimeter.
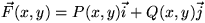 . Since
. Since 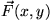 points in the direction that the wheel of the planimeter
is moving,
points in the direction that the wheel of the planimeter
is moving, 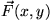 gives a scalar multiple of the velocity vector of the planimeter's
wheel. In terms of the planimeter, what interpretation would you assign to
the line integral
gives a scalar multiple of the velocity vector of the planimeter's
wheel. In terms of the planimeter, what interpretation would you assign to
the line integral
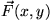 that describes the planimeter would be expected to be a
scalar multiple of
that describes the planimeter would be expected to be a
scalar multiple of

The point 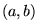 -- the location of the elbow of the planimeter -- can be expressed
in terms of
-- the location of the elbow of the planimeter -- can be expressed
in terms of 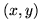 . You will find a command in your worksheet to solve for
. You will find a command in your worksheet to solve for ![]() and
and
![]() in terms of
in terms of ![]() and
and 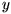 . The method is to realize that if the two "arms" of the planimeter
are the same length (say length 1), then the distance formula gives
. The method is to realize that if the two "arms" of the planimeter
are the same length (say length 1), then the distance formula gives
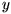 . Use these results to find a symbolic representation for the planimeter
vector field,
. Use these results to find a symbolic representation for the planimeter
vector field,
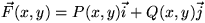 . How can you check to make sure that the vector
field you have defined is the right vector field for describing the planimeter?
. How can you check to make sure that the vector
field you have defined is the right vector field for describing the planimeter?
|
|
| modules at math.duke.edu | Copyright CCP and the author(s), 1999 |