The Equiangular Spiral
(Alternate Version)
Part 1: Background: Spirals in Nature
In this module you will discover some of the properties of a fascinating curve, the equiangular spiral, which abounds in nature -- there are shells, fossils, horns, nails, and hairs with spiral forms closely resembling this curve. Our investigation will focus on one of the most elegant of these examples, the shell of the chambered nautilus (Nautilus pompilius). Here is a picture* of a nautilus shell, together with a cross-section that shows the chambers from which it gets its name.
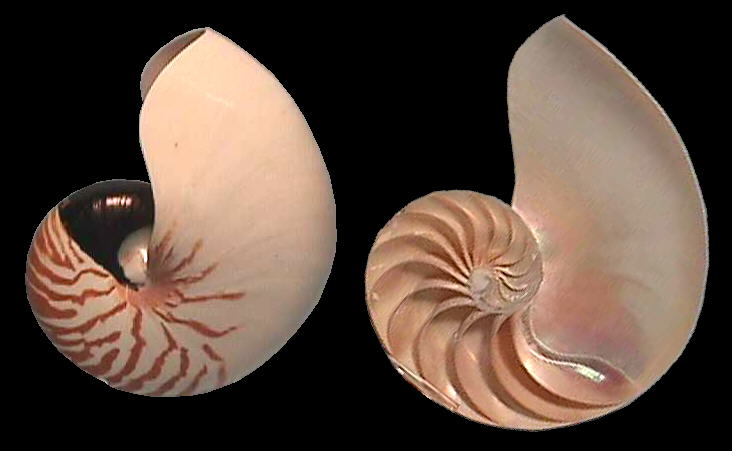
Why should the equiangular spiral be so prevalent in nature?
|
Aristotle, writing in about 350 BCE, noticed that certain things grow by adding units that are always the same shape, differing only in magnitude. Such shapes are called gnomons, and the study of "gnomonic growth" occupied a large part of Greek mathematics. We illustrate this idea with a growing spiral of isosceles right triangles, in which each new triangle has a leg that coincides with the hypotenuse of the preceding triangle. The most recent addition (shaded red) is a gnomon to the rest of the figure. Even in this very crude model we see something like a spiral pattern emerging.
|
|
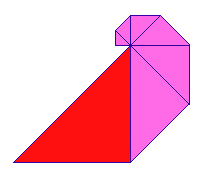
|
The British naturalist D'Arcy Thompson (On Growth and Form, 1917) observed gnomonic growth in many natural forms: "It is characteristic of the growth of the horn, of the shell, and of all other organic forms in which an equiangular spiral can be recognized, that each successive increment of growth is similar, and similarly magnified, and similarly situated to its predecessor, and is in consequence a gnomon to the entire pre-existing structure."
Here are some links to other sites at which you can pursue ideas related to gnomonic growth and equiangular spirals:
* Picture contributed by Bret Raines of The Molluscs Net

