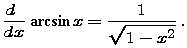Inverse Functions, Part 3

Inverse Functions

Part 3: Derivatives of Inverse Trig Functions

The inverse sine function is also called the arcsine function. In addition to the inverse notation sin^-1 x, the notations arcsin x and asin x are used. We will use the notation arcsin x, which you can think of as "the angle whose sine is x" -- with the understanding that the value of arcsin x (the angle) has to be in radian measure and has to be between - pi/2 and pi/2 (inclusive).

In Part 2 we constructed the inverse of the (restricted) sine function as a "function defined by an integral":

That is, arcsin x is a specific antiderivative of the integrand. In particular, we know already a derivative formula for the arcsine function:

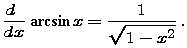
In this part we will see how find such a derivative formula directly. If we had known the derivative first, we could have constructed F(x) from that information -- instead of having it drop "out of the blue." Once the technique is clear, we will use it to find a formula for the inverse tangent function. Indeed, this is a technique that might be tried when looking for a formula for the inverse of any differentiable function.

Our starting point is the equation y = sin x. The inverse sine function is, by definition, the inverse of the function defined by that equation (with the domain restriction already noted). Thus, if we interchange x and y, we find that the inverse sine is defined by the equation x = sin y, with x as the independent variable and y as the dependent variable.

Differentiate implicitly the equation sin y = x, and solve for dy/dx. [This is a very easy calculation -- you can probably do it quicker with pencil and paper than with your computer algebra system.]
The result of step 1 involves cos y, which we need to express in terms of x. We know that sin y = x, and we know relationship between sin y and cos y. What is that relationship? Solve it for cos y in terms of sin y, and then replace sin y by x.
Don't be too hasty with that formula for cos y. Solving for cos y involves a square root, and we need to know whether to take the positive or negative square root. The following figures show the graph of cos y (with y as independent variable) in red and the graph of the positive square root of 1 - sin²y in blue. Where are their values the same? Where are they different? How is this related to the arcsine function? Did you make the right choice of sign in the preceding step?
Substitute the result from steps 2 and 3 into the result from step 1 to find an explicit formula for dy/dx as a function of x. Recall that, throughout this calculation, y has been an abbreviation for arcsin x. Thus, you should now have a formula for the derivative of the arcsine function. Does it agree with the one we gave above?
Explain in your own words where the integral formula for arcsin x came from.

We turn our attention now to the tangent function and its inverse -- specifically to the task of finding the derivative of its inverse.

The following figure shows three periods of the tangent function. How should we restrict the domain in order to have an invertible function?
What is the relationship between tan x and sec x? You will need this in the next step. [If you don't remember, you can derive it from the relationship between sin x and cos x.]
The inverse of the tangent function (arctangent, denoted arctan x) satisfies the equation tan y = x, where x is the independent variable, and y is the dependent variable. Use the implicit differentiation technique developed above to find a formula for the derivative of arctan x as an explicit function of x.