|
|
|
|
|
|
In this module we model the vibrations of stretched string of length L. (Think of an idealized violin or guitar string.) We impose a coordinate system with x = 0 corresponding to the left end and x = L corresponding to the right. We assume that the vibrations occur in the vertical plane above and below the string's resting position, and we let y(x,t) be the vertical displacement of the string at time t and position x.

The motion of the string is governed by the one-dimensional wave equation:

Since the ends of the string are fixed, we look for solutions of this equation that satisfy the boundary conditions:

Before we tackle the full generality of this problem, we consider first a simpler vibrating string problem with the following characteristics:
Graph of tent function f(x)

So now we are looking for y(x,t) satisfying

In this case, the solution has the symbolic form
Now we return to the finite-string problem and assume that the string is tied down at x = 0 and x = L. We continue to assume that the initial displacement is the tent function f, and the initial velocity is 0. Thus, we want to find a function y that satisfies these three conditions:
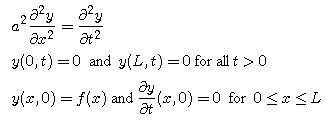
We may describe the solution to this problem by a "traveling wave" as well. The trick is to think of the string as still infinite with alternating positive and negative copies of the initial condition on succesive intervals of length L. In our example, we'll take L = 4.
|
|
|
| modules at math.duke.edu | Copyright CCP and the author(s), 1999-2001 |