|
|
|
|
|
|
In this part we consider the approximation of functions of period 2L by appropriate trigonometric polynomials. (Even though we are considering periods of any positive length, we will find it convenient to express the periods as multiples of 2.) Our first task will be to identify the appropriate sine and cosine functions to use in this case.

where the coefficients are given by

List the changes necessary to obtain these coefficient formulas from the ones for 2 pi-periodic functions.
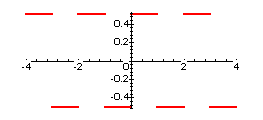
How do you know you will only need sine terms in the expansion? Compare the graphs of the approximations for n = 1 to 10 to the graph of the step function.
|
|
|
| modules at math.duke.edu | Copyright CCP and the author(s), 1999-2003 |