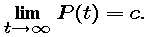Logistic Growth Model

Part 2: Equilibria

1. The interactive figure below shows a direction field for the logistic differential equation

   

   as well as a graph of the slope function, f(P) = r P (1 - P/K). Click on the left-hand figure to generate solutions of the logistic equation for various starting populations P(0). [Note: The vertical coordinate of the point at which you click is considered to be P(0). The horizontal (time) coordinate is ignored.]

2. Explain why P(t) = 0 is a solution. A constant solution is called an equilibrium.

3. The logistic equation has another equilibrium, i.e., a solution of the form P(t) = constant. What is the constant? Explain how you know from the differential equation that this function is a solution.

4. If the starting population P(0) is greater than K, what can you say about the solution P(t)? What do you see in the differential equation that confirms this behavior?

5. If the starting population P(0) is less than than K, what can you say about the solution P(t)? What do you see in the differential equation that confirms this behavior?

6. Why is carrying capacity an appropriate name for K?

An equilibrium solution P = c is called stable if any solution P(t) that starts near P = c stays near it. The equilibrium P = c is called asymptotically stable if any solution P(t) that starts near P = c actually converges to it -- that is,

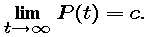
If an equilibrium is not stable, it is called unstable. This means there is at least one solution that starts near the equilibrium and runs away from it.

7. Is the equilibrium solution P = 0 stable or unstable? If stable, is it also asymptotically stable? Explain.

8. Is the equilibrium solution you found in step 3 stable or unstable? If stable, is it also asymptotically stable? Explain.

---