Gain and Phase Shift

Part 1: Background: A Damped Forced Oscillator

In this module we study the relationship between "input" and "output" for a damped harmonic oscillator (mechanical, electrical, electronic) modeled by the differential equation

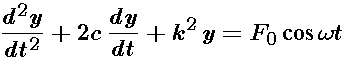
where c and k are nonnegative constants with c < k. Note that we have written the damping coefficient as 2c and the "spring constant" as k² to simplify expressions involving the characteristic roots (eigenvalues). Specifically, those roots are

so the solutions of the homogeneous equation

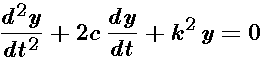
are all of the form

This is the transient part of any solution. The transient decays exponentially to 0, and we are left with the steady state solution. This is illustrated in the following figure, which shows the solution of the initial value problem

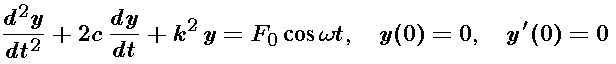
where c = 1, k = 2, F₀ = 5, and omega = 2.

We call the driving function, F₀ cos(omega t), the input function, and we call the steady state solution the output function. We refer to omega as the driving frequency or input frequency, although technically the frequency is omega/(2 pi).

The steady state solution has the form

Direct calculation shows that the coefficients A and B are

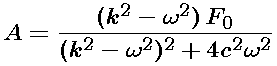
and

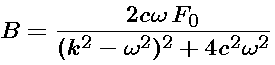
If we factor out

we see that the steady state solution can be written as

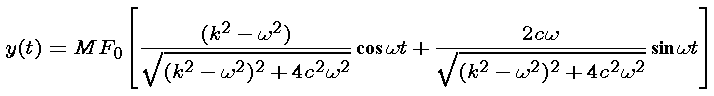
where

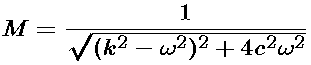
Now the coefficients of cos(omega t) and sin(omega t) are numbers whose squares add up to 1. Thus, we can consider those numbers to be cosine and sine of some angle phi. That is, the solution has the form

We can apply the formula for cosine of a difference of two angles to write

Thus, we see that the steady state solution is a sinusoidal function with the same frequency as the input function, shifted to the right by phi/omega radians on the t-axis. The ratio M of the output amplitude MF₀ to the input amplitude F₀ is called the gain, and phi is called the phase shift.

1. Explain why gain M and phase shift phi are independent of the initial conditions y(0) and y'(0).
2. Explain why

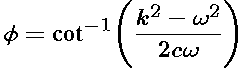
We choose to write the formula for phi in terms of an inverse cotangent rather than an inverse tangent because c and omega must both be nonzero, but we haven't ruled out the possibility that omega is equal to k.