Introduction to the One-Dimensional Heat Equation*

Part 1: A Sample Problem

In this module we examine solutions to a simple second-order linear partial differential equation -- the one-dimensional heat equation -- which models the flow of heat in a rod that is insulated everywhere except at the two ends. Solutions of this equation are functions of two variables: position along the rod and time. The "one-dimensional" in the description of the differential equation refers to the fact that we are considering only one spatial dimension.

Imagine a thin rod that is given an initial temperature distribution, then insulated on the sides. The ends of the rod are kept at the same fixed temperature -- e.g., suppose at the start of the experiment, both ends are immediately plunged into ice water. We are interested in how the temperatures along the rod vary with time. Suppose that the rod has a length L (in meters), and we establish a coordinate system along the rod as shown here.

Let u(x,t) represent the temperature at the point x meters along the rod at time t (in seconds). We start with an initial temperature distribution u(x,0) = f(x) such as the one represented by the following graph (with L = 2 meters).

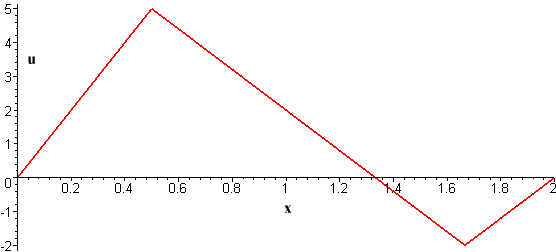
The partial differential equation

is used to model one-dimensional temperature evolution. We will not discuss the derivation of this equation here. The most important features of this equation are the second spatial derivative u_xx and the first derivative with respect to time, u_t. The positive constant a² represents the thermal diffusivity of the rod. It depends on the thermal conductivity of the material composing the rod, the density of the rod, and the specific heat of the rod.

1. Explain why the units of a² must be (length)² / time.

Typical values for the diffusivity constant are given in the table below (from Boyce and DiPrima, Elementary Differential Equations and Boundary Value Problems, 6th ed.)

The function u(x,t) that models heat flow should satisfy the partial differential equation. However, in addition, we expect it to satisfy two other conditions. First, we fix the temperature at the two ends of the rod, i.e., we specify u(0,t) and u(L,t). In our sample problem, we will assume that both ends are kept at 0 degrees Celsius:

This is called a boundary condition since it is imposed on the values of the desired function at the boundaries of the spatial domain.

The remaining condition represents the initial temperature distribution

where f(x) is the temperature at position x at time t=0. All together, the model function u(x,t) that we seek should satisfy

In this module we are not concerned with finding symbolic descriptions of the solutions of such problems. Rather, we will look graphically at the solutions to see

• how they evolve in time;
• how they depend on the boundary conditions;
• how they depend on the initial condition.

2. Sketch what you think the temperature distribution u(x,t₁) will be a short time after the start, at t = t₁. What will the distribution be after a somewhat longer time? Do you think that the temperature distribution will approach a steady state?
   
3. Use the applet below to display the graphs of temperature as a function of distance x at several different times t. Do these graphs agree with your intuition?
   




Temperature of the Rod


4. So far we have looked at just one way of representing the time evolution of temperature -- "snapshots" of the temperature along the rod at various fixed times. Another way to represent this evolution is to fix x (i.e., pick a particular spot on the rod) and examine the graph of the temperature at that spot as a function of time. Pick several different values of x and sketch what you think the graph of the temperature as a function of time will be at that spot. Then use the applet below to display the graphs. (Move the slider to change the value of x.)




Temperature vs. Time


5. We may also look at the graph of the temperature function u as both x and t vary. This surface can be thought of as an infinite number of time snapshots stacked up one after the other. Identify on this surface each of the curves you obtained in Steps 3 and 4.